天线入门¶
第一章 引言¶
1.1 如何阅读符号和记号¶
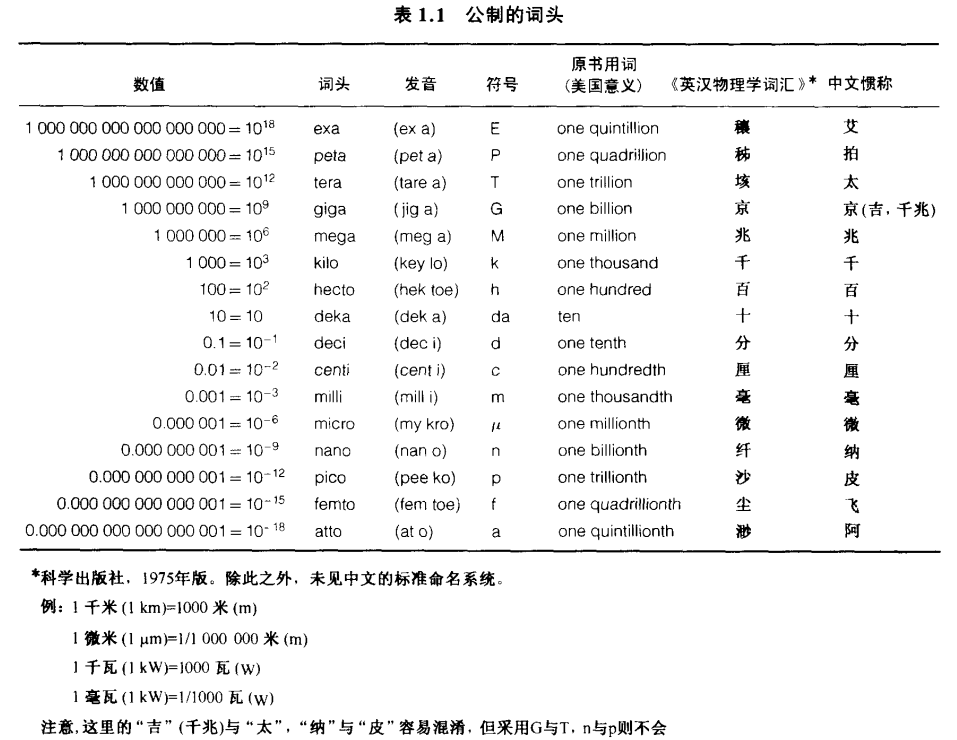
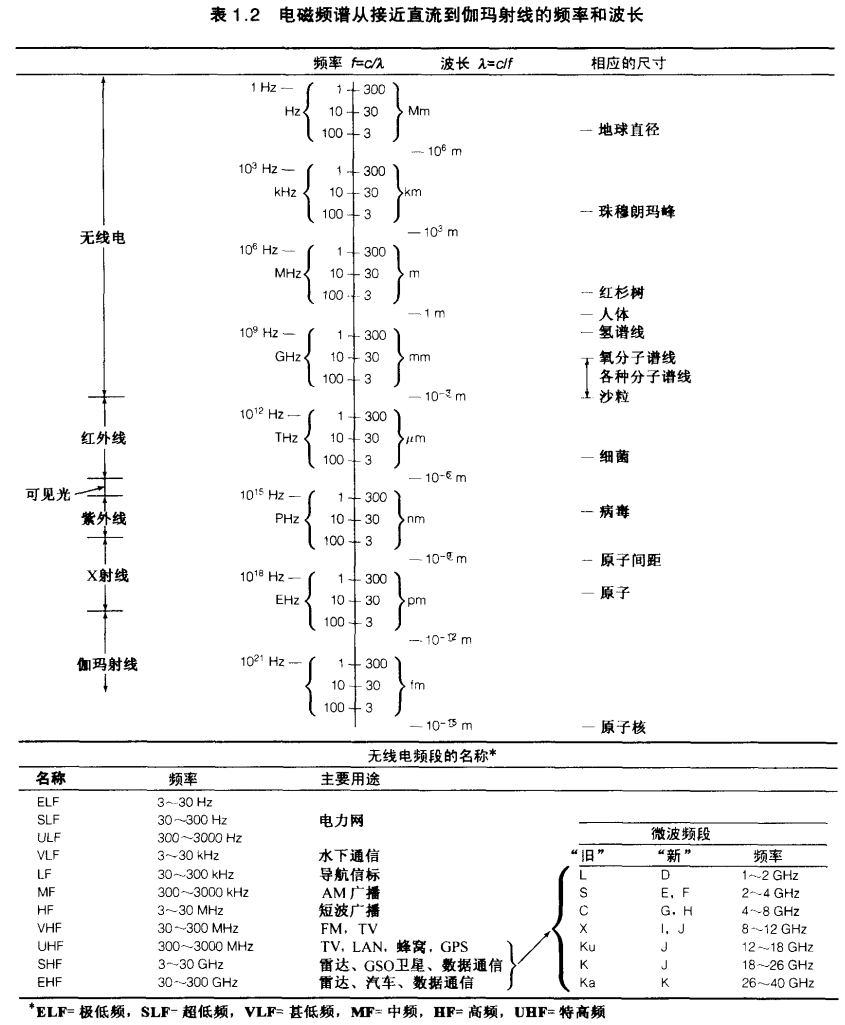
1.2 无线频谱与无线电频段¶
第二章 天线基础¶
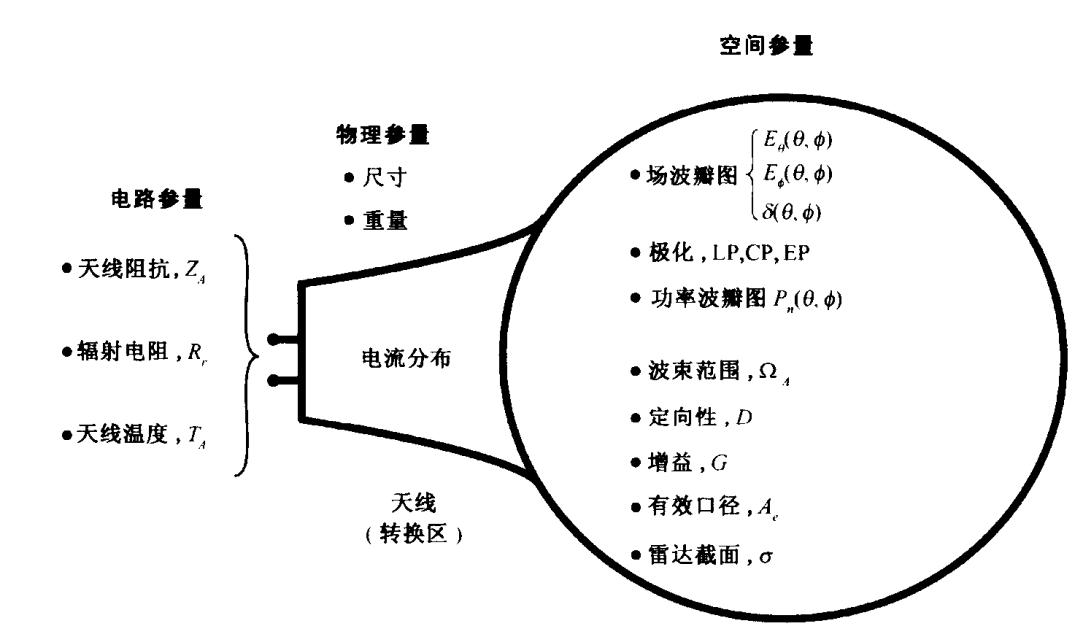
2.1 基本天线参量¶
什么是天线?¶
天线可被定义为一种附有导行波与自由空间波相互转换区域的结构,是一种导行波与自由空间波之间的转换器件或者换能器。
基本辐射方程¶

辐射电阻¶
可以理解为一种物理上并不存在的“视在”电阻,是将天线耦合到远处空间的“视在”传输线的一个量。
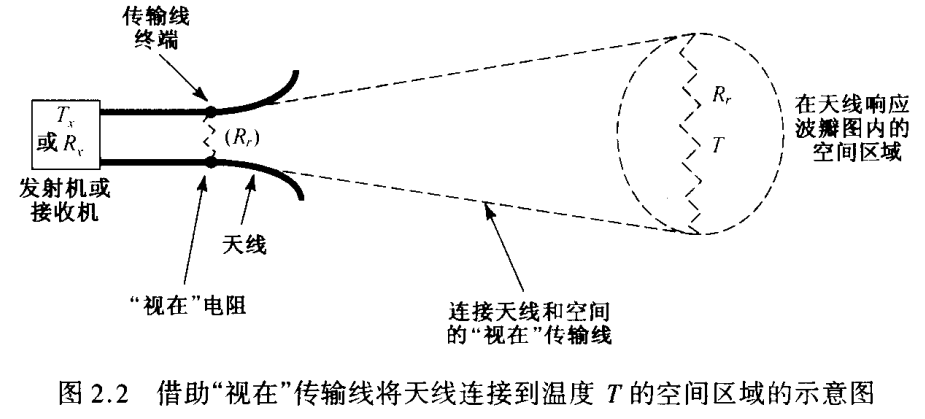
2.2 波瓣图¶
要完整的说明矢量场强的辐射波瓣图,需要用到三幅图形:
1.电场的\(\theta\)分量作为角度\(\theta\)和\(\phi\)的函数\(E_{\theta }( \theta , \phi ) ( \mathcal{V} \mathrm{~m}^{- 1})\),如图 2.3 和图 2.4 所示;
2.电场的\(\phi\)分量作为角度\(\theta\)和\(\phi\)的函数\(E_{\phi }( \theta , \phi ) ( \mathcal{V} \text{ m}^{- 1}) ;\)
3.这些场分量的相位也是\(\theta\)和\(\phi\)的函数\(\delta_{\theta}(\theta,\phi)\)和\(\delta_{\phi}(\theta,\phi)(\)弧度或度)。
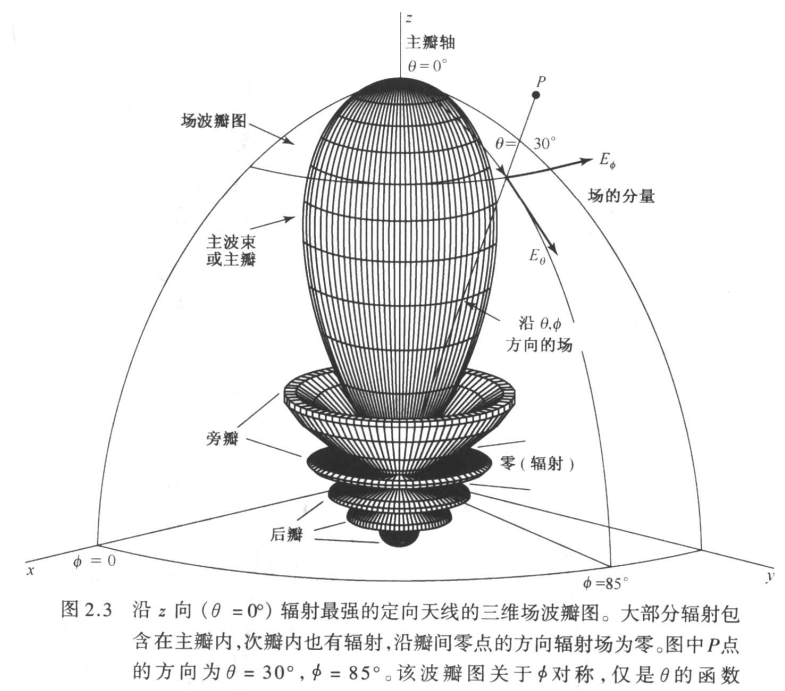
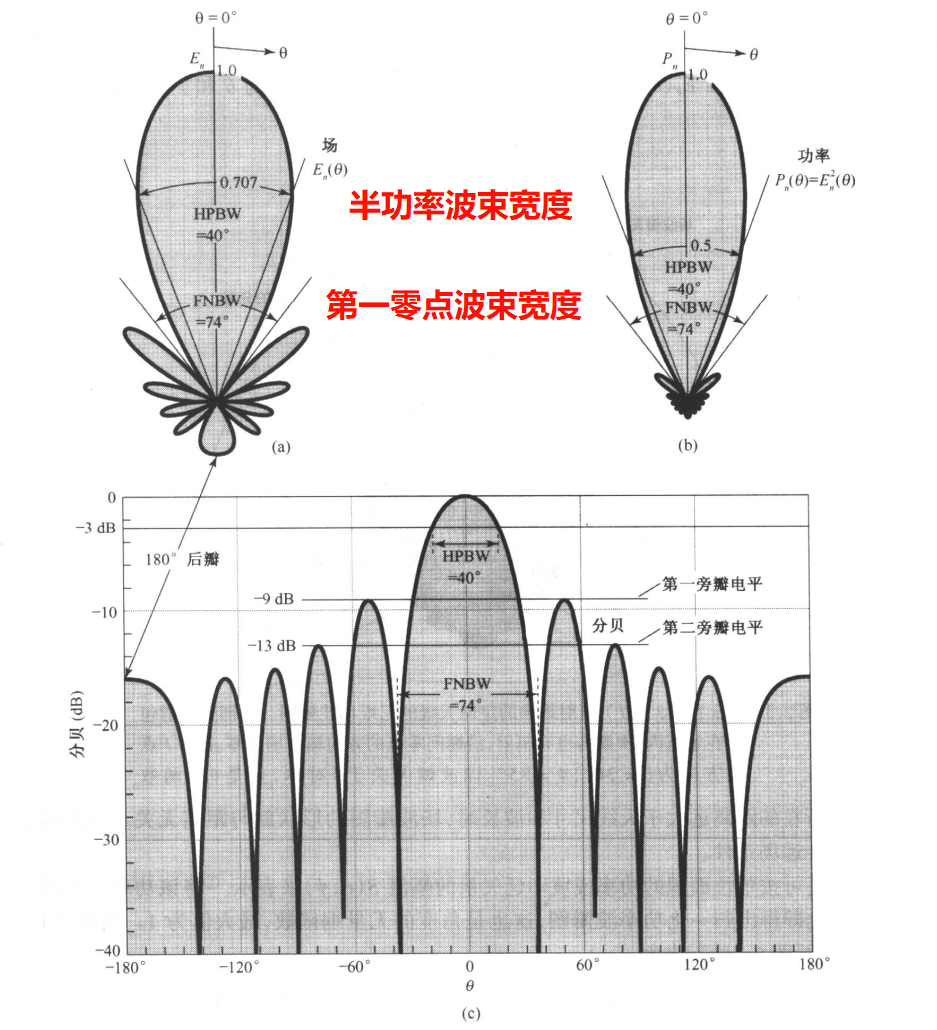
图6 三维天线波瓣图(图 2.3)的二维场、功率和分贝图。(a)场波瓣图(正比于电场\(E\),V\(m^{- 1})\)。在\(\theta=0^{\circ}\)方向上归一化场\(E_n(\theta)=1\), 由 \(E=0.707\)电平测得半功率波束宽度(HPBW)=40°;(b)功率波瓣图(正比于\(E^2\))。在\(\theta=0^\circ\)方向上\(P_n=1\),由\(P_n=0.5\)电平测得半功率波束宽度( HPBW)\(=40^{\circ};(\)c)场波瓣的分贝( dB)图。在-3dB处测得( HPBW)\(=40^\circ\)。在-9dB处测得第一旁瓣,在-13dB处测得第二旁瓣。分贝图能够很好地显示较小的旁瓣
波束宽度(HPBW)¶
符合远场条件¶
凡场点所在的距离远大于天线尺寸和波长时,场波瓣图的形状就与距离无关。通常称此类波瓣图符合远场条件。
归一化波瓣图¶
归一化场波瓣图
归一化功率波瓣图
式中 \(S(\theta,\phi)=\)坡印廷矢量的幅值\(=[E_\theta^2(\theta,\phi)+E_\phi^2(\theta,\phi)]/Z_0\),W m\(^{-2}\) \(S(\theta,\phi)_{\mathrm{max}}=S(\theta,\phi)\)的最大值,W m\(^{-2}\) \(Z_0=\)空间的本征阻抗\(=376.7\Omega\) 其分贝电平则得自
式中 \(P_n(\theta,\phi)\)得自归一化功率波瓣图
注意,这里的坡印廷矢量方向在远场区是朝外的径向。
2.3 波束范围与波束立体角\(\Omega_A\)¶
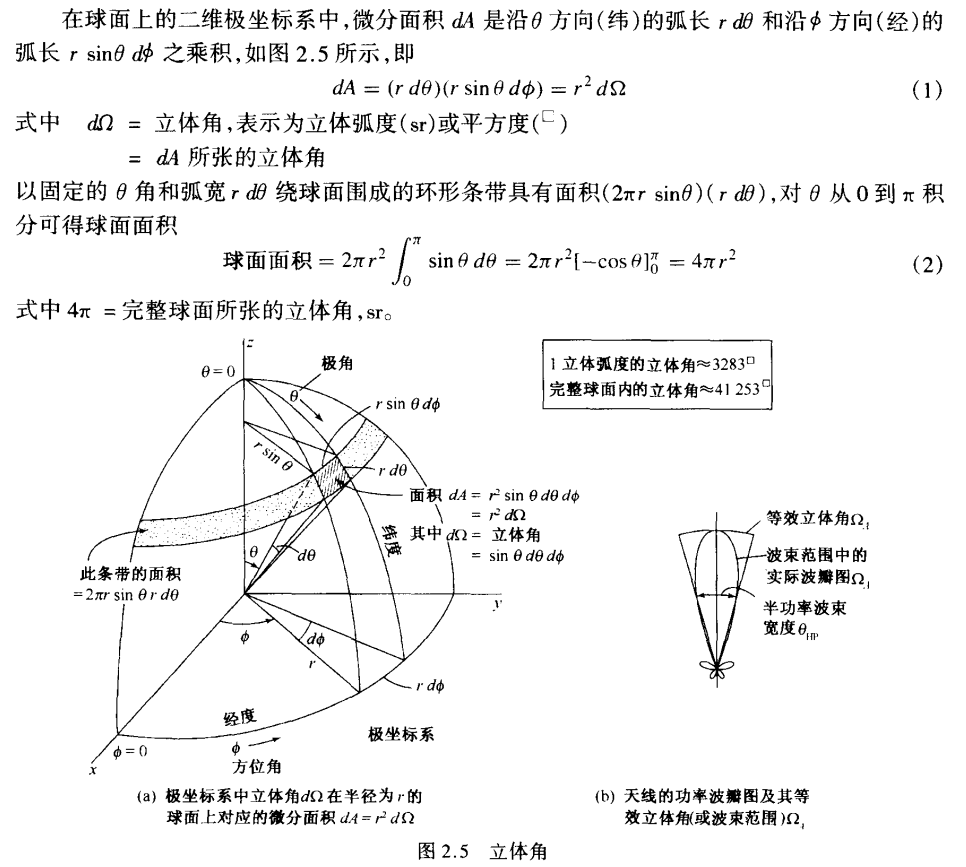

2.4 辐射强度¶
每单位立体角内由天线辐射的功率称为辐射强度 \(U(\mathbf{W}\) sr\(^-1\),瓦每立体弧度;或 W deg\(^-2\),瓦每平方度)。前节所述的归一化功率波瓣图也能表示成辐射强度\(U(\theta,\phi\) )的归一化函数形式
与坡印廷矢量(幅值) S 反比于(自天线的)距离的平方不同,辐射强度\(U\)与此距离无关。这里均假设为天线的远场情况(参见 2.13 节) [link]
2.5 波束效率¶
(总)波束范围 \(\Omega_A(\)或波束立体角)由主瓣范围(或立体角)\(\Omega_M\) 加上副瓣范围(或立体角)\(\Omega_m\)所构成(如果主波束并不是由深零值所界定的,其延伸部分就变得难以判断了),即
主波束范围与(总)波束范围之比称为(主)波束效率\(\varepsilon_n\),即
副瓣范围与(总)波束范围之比称为杂散因子,即
显然,
2.6 定向性D和增益G¶
天线的定向性是在远场区的某一球面上最大辐射功率密度\(P(\theta,\phi)_{max}(Wm^{-2})\)与其平均值之比,是大于等于1 的无量纲比值,可以写成
其中,球面上的平均功率密度为
因此,定向性又可以写成
和
式中\(P_n(\theta,\phi)d\Omega\)是归一化功率波瓣图,即定向性又等于球面范围与天线的波束范围之比。
由计算公式可以知道,波束范围越小,则定向性越高。例如,一个天线仅对上半空间辐射,其波束范围\(\Omega_A=2\pi\ sr\),则定向性为 $$ D=\frac{4\pi}{2\pi}=2(=3.01dBi) $$ 式中dBi为相对于各向同性的分贝数。
Example
如果已知某天线的半功率波束宽度,则其定向性还可以表示为
这意味着该天线沿主向辐射的功率是相同输入功率下非定向的各项同性天线的100倍。
在2.8节中,还将接触到一个来自口径的定向性,在这里为了保持完整性直接列出,相关定义见2.8节。

天线增益是一个实际的参量,该参量因天线或天线罩的欧姆损耗而小于定向性。在发射情况下,天线增益还包括向天线馈送功率的损耗。这种损耗不意味着辐射,而是加热天线结构。天线的失配也会减小增益。增益与定向性之比是天线效率因子。这种关系可以表示为: $$ G=kD $$ 这里,\(k(0\leq k \leq 1)\)是无量纲的。
一个天线的增益可以由与一个已知增益的参考天线在相同输入功率下获得的最大辐射功率密度的比值确定,即 $$ \mathrm{Gain}=G=\frac{P_{\max}(\mathrm{AUT})}{P_{\max}(\text{参考天线})}\times G(\text{参考天线}) $$
计算定向天线的增益

2.7 定向性与分辨率¶
天线的分辨率(通常称为瑞利分辨率)可以定义为第一零点波束宽度的一半,即FNBW/2(事实上,FNBW/2稍大于HPBW)。例如,当天线的FNBW=2°的时候,具有1°的分辨率。
由天线波束范围的定义可以得到,
因此,天线能够分辨出均匀分布于天空的无线电发射机或者电辐射源的数目N的近似值为
于是可以得到概念化的结论:天线能够分辨的点源数目在数值上等于该天线的定向性,即\(D=N\)。在均匀源分布的理想情况下,定向性等于天空中天线所能分辨的点源数(点源在球面上的严格规则分布只可能对应于正多面体顶点的4,6,8,12,或者20点)。
2.8 天线口径¶
假设接收天线是置于均匀平面电磁波中的矩形电磁喇叭,记平面波的功率密度即坡印廷矢量的幅度为S(\(W m^{-2}\)),喇叭的物理口径面积为\(A_p(m^2)\),如果喇叭以整个物理口径从来波中摄取所有功率,则喇叭的吸收总功率为 $$ P=\frac{E^2}{Z}A_p=SA_p (W) $$ 于是可以认为电磁喇叭从来波中提取的总功率正比于某一种口径的面积。
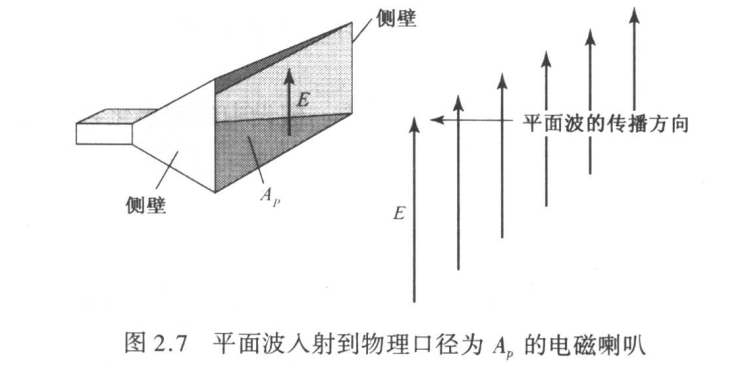
口径效率定义为有效口径和物理口径的比值,即 $$ \varepsilon_{ap}=\frac{A_e}{A_p} (无量纲) 口径效率 $$
Note
对于喇叭和抛物面反射镜天线而言,口径效率普遍在50%到80%的范围内。而对于在物理口径边缘也能维持均匀场的偶极子或者贴片大型阵列来说,口径效率可以接近100%。然而要降低旁瓣必定采用边缘锥削的口径场分布,导致口径效率的下降。
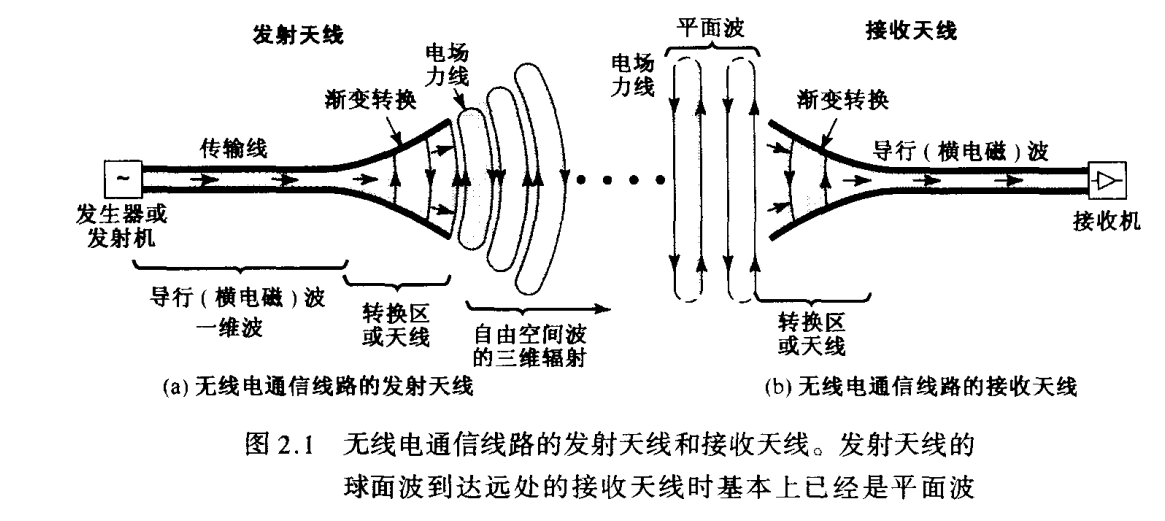
假设有一个有效口径为\(A_e\)的天线,其全部功率按照波束范围为\(\Omega_A(sr)\)的圆锥形波瓣辐射。如果口径上有均匀场\(E_a\),则其辐射功率为
\[ P=\frac{E_a^2}{Z_0}A_e \]式中的\(Z_0\)是媒质的本征阻抗,在空气或者真空中为377Ω。
假定在距离为\(r\)处有均匀的远场\(E_r\),则辐射功率还可以写成
\[ P=\frac{E_r^2}{Z_0}r^2\Omega_A\quad\mathrm{(W)} \]
口径面积-波束范围的关系式
因此当波长给定的时候,可以由已知的等效口径面积确定波束范围。则可以得到来自口径的定向性表达
任何天线都有其有效孔径,或得自计算,或得自测量。
Example
假设理想化各向同性天线,因其定向性D=1,其有效口径为
所有无损耗的天线必然具有一个等于或大于此值的有效口径。根据互易性原理,一个天线的有效口径在发射状态和接收状态时相同的。
2.9 有效高度¶
有效高度是另一个与口径有关的参量,有效高度乘上与之相同极化的入射电场,就得到感应电压V,即
另一种定义有效高度的途径是考虑天线的发射状态,于是有效高度等效于物理高度(或者长度l)乘上(归一化)平均电流,即
有效高度还可以跟普遍地表示成适合任何极化状态的矢量形式,即
显然,有效高度对于塔型发射天线来说是非常重要的参量,对于小天线也很有用。
有效口径和有效高度之间有以下简单关系。
对于辐射电阻\(R_r\)与负载匹配的天线,注入其负载的功率等于
当采用有效口径表示的时候,有
两者相等得到两者之间的关系:
因此,有效高度与有效口径之间的关系还取决于天线的辐射电阻和空间的本征阻抗。
短偶极子天线的有效口径和定向性
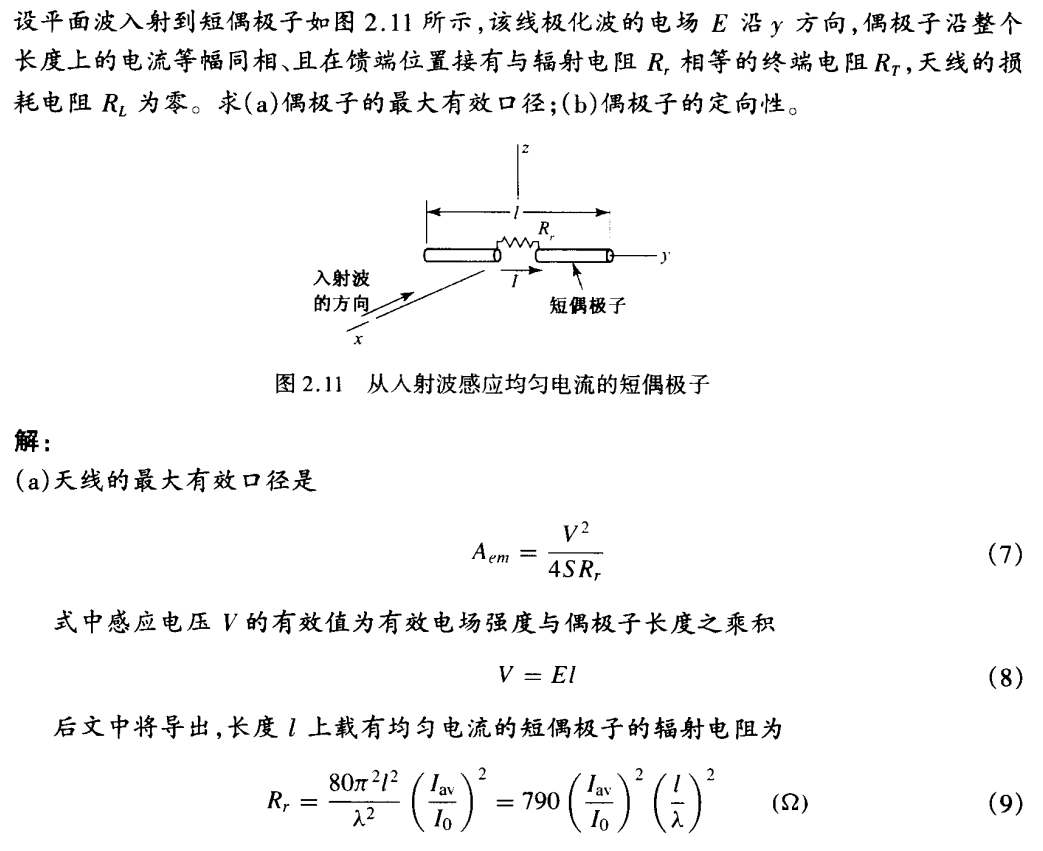

一个典型的短偶极子长\(\lambda/10\)而直径为\(\lambda/100\),其物理的截面口径0.001\(\lambda^2\)。比较上面你的例题,可以看到简单偶极子或直线天线可以具有比有效口径更小的物理口径。根据天线类型的不同,其有效口径可以大于或小于其物理口径。
线状\(\lambda/2\)偶极子的有效口径和定向性
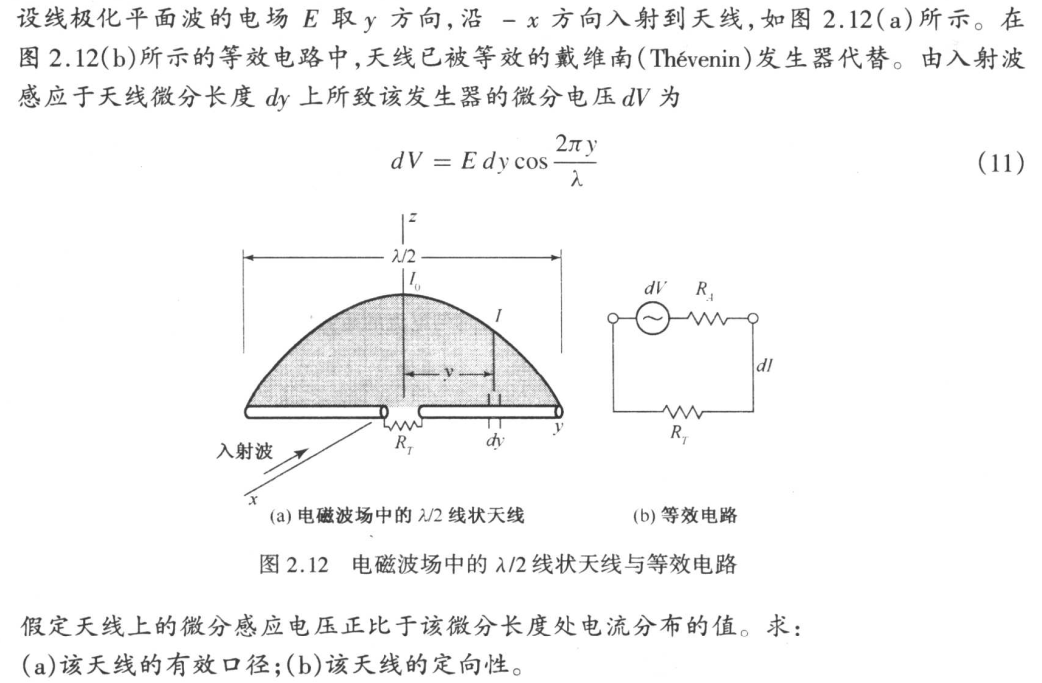 (a)总的感应电压为微分电压沿天线长度的积分,可以写成
(a)总的感应电压为微分电压沿天线长度的积分,可以写成

Note
虽然天线的辐射电阻、有效口径、有效高度和定向性在接受和发射状态下是相同的,但是通常其电流分布式不同的。所以,平面电磁波在接受天线上激起的电流,其分布有别于在该天线的端对上施加电压的情况。
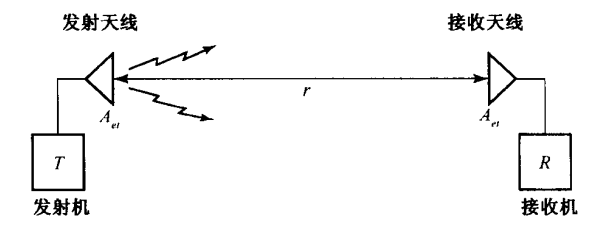
2.10 无线电通信线路¶
弗里斯传输公式
用于确定无线电通信线路中被无损耗且与负载匹配的天线所接收的功率
已知无损耗、已匹配、有效面积为\(A_{er}\)的接受天线所手机的功率为
又发射天线的增益
带入后可以得到弗里斯传输公式
式中,\(P_r\)为接收功率,\(P_t\)为发射功率,\(A_{er}\)为接收天线的有效口径,\(A_{et}\)为发射天线的有效口径,\(r\)为两天线之间的距离,\(\lambda\)为波长。
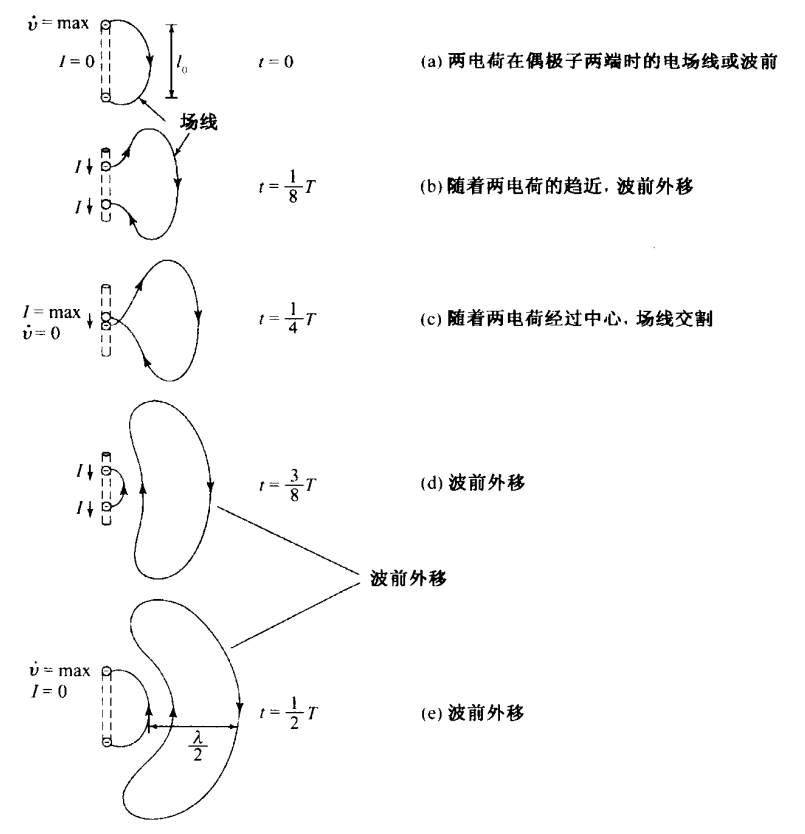
2.11 振荡偶极子产生的场¶
虽然电荷沿直的导体匀速运动不会产生辐射,但是当做简谐加速运动的时候就会形成辐射。考虑两个等量异性且按瞬时间距\(l\)(最大间距为\(l_0\))上下简谐振荡运动的电荷,观察其电场的变化。
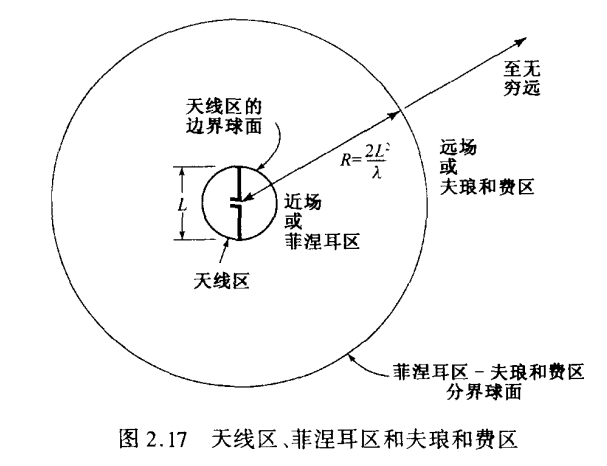
2.12 天线的场区¶
围绕着天线的场可以划分为两个主要的区域,接近天线的区域称为近场(菲涅尔区),离天线较远的称为远场(夫琅和费区)。两者的分解可取半径为 $$ R=\frac{2L^2}{\lambda} $$ 式中,\(L\)表示天线的最大尺度,\(\lambda\)为工作波长。
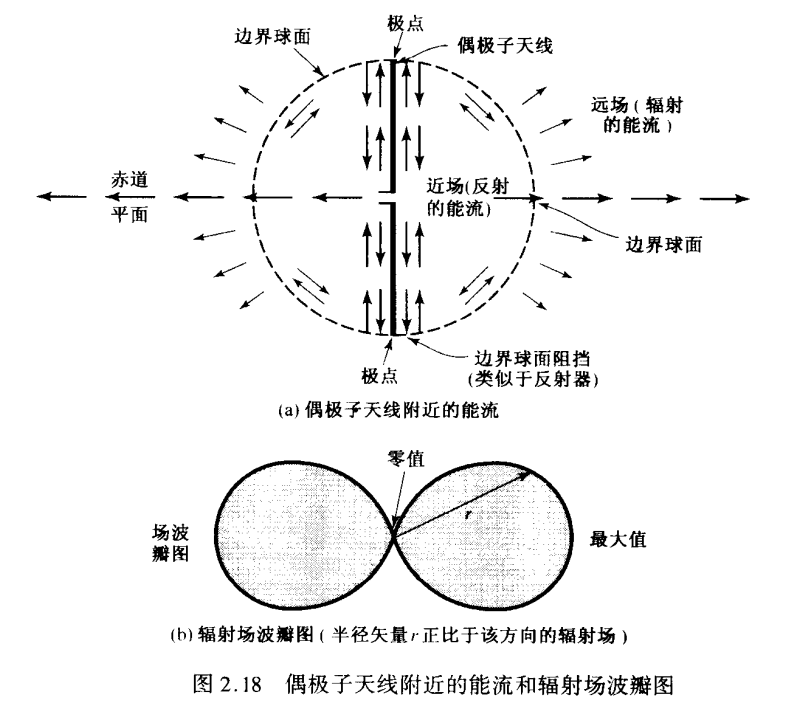
在远场区,测得场分量处于辐射方向的横截面内,所有的功率流都是沿径向向外的。在近场区内,电场有显著的径向分量,其功率流不完全是径向的,场波瓣图通常依赖于距离。
Note
对于半波长偶极子天线,某一瞬间的能量储存与接近天线末端即最大电荷区为主的电场中,经半个周期的转换之后,又储存于接近天线中心即最大电流区为主的磁场中。
2.13 形状--阻抗的讨论¶
Note
具有大而突变的不连续性的天线具有大的反射,并且只能在窄频带上借抵消反射而用作无反射的电磁波转换器
具有小而渐变的不连续性的天线具有小的反射,并且通常能在较宽频带上直接用作无反射的电磁波转换器。
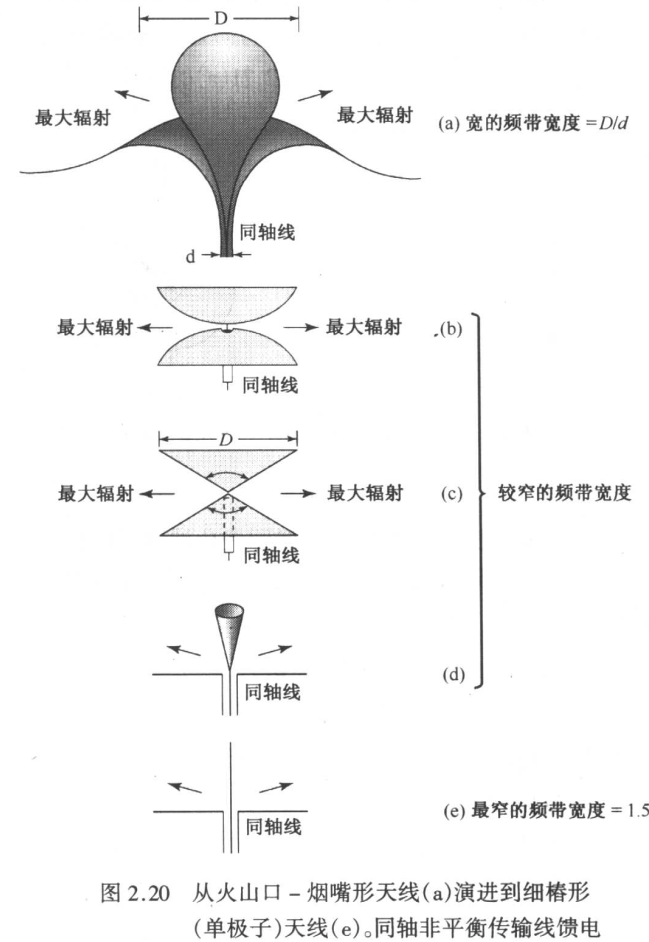
随着天线从基本型式的一步步演进,传输线的不连续性也越发突出,最终成为地平面与同轴线的接头,这将使得部分能量反射回传输线。天线越细,其末端的反射越大,在某些频率上,这两种反射可以补偿,但补偿的带宽很窄。
2.14 线极化、椭圆极化和圆极化¶
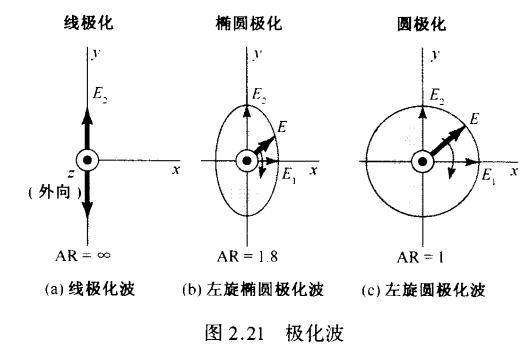
考虑由纸面向外的行进的平面波,将电场矢量\(E\)作为时间的函数,随时间而变化,其矢尖描绘出的路径为极化椭圆
a的电场始终沿着y方向,被称为是y方向线极化的。其电场作为时间和位置的函数,可以写成
更一般的,如b的电场有y分量和x分量,且两个分量之间存在相位差,这种波被称为是椭圆极化的。这种椭圆的长轴和短轴之比称为轴比(AR,Axial Ratio),可以表示为\(AR=E_2/E_1\)。椭圆极化的两种特殊情况即圆极化和线极化。
极化椭圆的标准方程¶
对于极化椭圆,取任意方向的一般椭圆极化波,可用分别沿着x方向和y方向的两项线极化分量来描述,即
其中,\(\delta\)是\(E_y\)滞后于\(E_x\)的时间-相位角。
瞬时的总矢量场\(\mathbf{E}\)
当\(z=0\)处,展开\(E_y\)
由\(E_x\)的关系式将上式中的三角函数用\(E_x\)和\(E_1\)表示,整理出
或者用\(\sin^2{\delta}\)归一化,可以得到如图极化椭圆
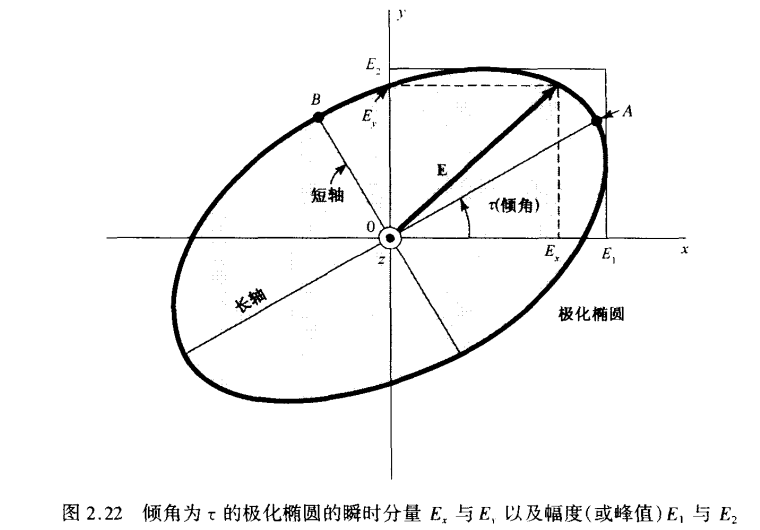
则轴比定义为 $$ AR=\frac{OA}{OB} $$
极化方式¶
线极化
\(E_1=0\),则波是沿\(y\)向线极化的
\(E_2=0\),则波是沿\(x\)向线极化的
\(E_1=E_2,\delta=0\),则波是沿\(\tau\)向线极化的
圆极化
左旋圆极化
\(E_1=E_2,\delta=+90°\)
判断方法:左手大拇指为波的传播方向,总矢量场方向随时间沿手指围绕方向旋转。
右旋圆极化
\(E_1=E_2,\delta=-90°\)
判断方法:右手大拇指为波的传播方向,总矢量场方向随时间沿手指围绕方向旋转。
Note
除非指定波的传播方向,否则极化的左旋或者右旋就是模棱两可的。
2.15 椭圆和圆极化波的坡印廷矢量¶
坡印廷矢量的复数表示为
平均坡印廷矢量\(\mathbf{S_{av}}\)为其实部,因此可以写成
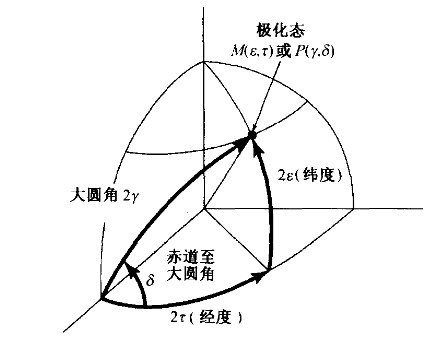
2.16 极化椭圆和庞加莱球¶
用庞加莱球表示波的极化,就是用该球面上的点来描述波的极化状态。该点的经度和纬度与极化椭圆的参量有下列关系: $$ \begin{array}{c}\text{经度}=2\tau\\text{纬度}=2\varepsilon\end{array} $$ 其中\(0^{\circ}\leq\tau\leq180^{\circ};^{①}\varepsilon=\tan^{-1}(1/\mp\mathrm{AR}),-45^{\circ}\leq\varepsilon\leq+45^{\circ}\);轴比(AR)和\(\varepsilon\)角在左旋时为正,右旋时为负。
第三章 天线家族¶
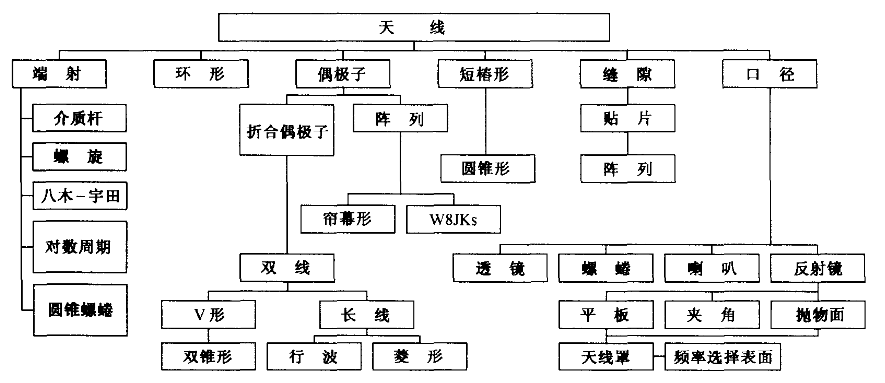
3.1 引言¶
- 基本类型
- 环形、偶极子和缝隙
- 张开的同轴线、双线和波导
- 反射镜与口径类型
- 端射与宽频带类型
- 镶板式、缝隙和栅格阵列
Note
对大多数天线来说,其损耗甚小,其增益可近似等于定向性,因而在实际问题中往往混用增益和定向性。